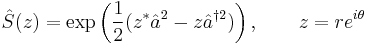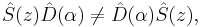Squeeze operator

Quantum optics operators
Ladder operators
Creation and annihilation operators
Displacement operator
Rotation operator (quantum mechanics)
Squeeze operator
Anti-symmetric operator
Quantum correlator
Hanbury Brown and Twiss effect
[edit this template]

In quantum physics, the squeeze operator for a single mode is[1]

\hat{S}(z) = \exp \left ( {1 \over 2} (z^* \hat{a}^2 - z \hat{a}^{\dagger 2}) \right ) , \qquad z = r e^{i\theta}

where the operators inside the exponential are the ladder operators. The squeeze operator is ubiquitous in quantum optics and can operate on any state. For example, when acting upon the vacuum, the squeezing operator produces the squeezed vacuum state.

The squeezing operator can also act on coherent states and produce squeezed coherent states. The squeezing operator does not commute with the displacement operator:

\hat{S}(z) \hat{D}(\alpha) \neq \hat{D}(\alpha) \hat{S}(z),

nor does it commute with the ladder operators, so one must pay close attention to how the operators are used.

See also

References

  1. ^ Gerry, C.C. and Knight, P.L. (2005). Introductory quantum optics. Cambridge University Press. p. 182. ISBN 9780521527354. http://books.google.com/books?id=CgByyoBJJwgC&pg=PA182.